今のお金も利回りで増やせば・・・

金融リテラシー講座　「金利計算、利回り計算のやり方」６回

フィナンシャル・アドバイス代表　井上　明生

前回の式2－④は投資後の受取りキャッシュフローを利回りで割り引いたものが債券単価になることを示したものですが、償還までの期間が長い債券ほど計算式が長くなります。７年債くらいならなんとかなりますが、20年債や30年債になると大変です。
式２－④は、利息部分と償還金部分に分けると次のように短くできます。

これに償還金部分の現在価値を足したものが債券単価となります。

債券単価を求める一般的な式としては、

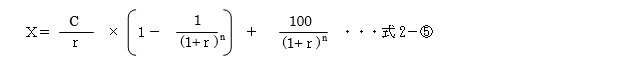
となります。ただし、毎年の利息100 R＝Cとし、ｎ年後に償還される債券の場合です。年2回利払いがある債券を半年複利利回りで計算する場合は、Cとｒを2分の1にし、ｎを2ｎとして計算します。

この講座（第二部）の第1回で米国債ストリップ債の話をしました。債券には利付債だけではなくストリップ債のように償還まで期中に利息のない割引債のかたちで発行あるいは流通している債券もあります。償還までｎ年の割引債券として、利回りｒ（年複利利回り）と債券単価Ｘとの関係はつぎのようになります。

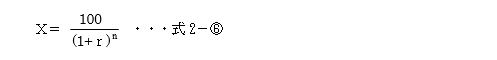
割引債の場合途中の利息がなく償還金だけですから計算式はシンプルです。
これを使って第1回に紹介した米国債ストリップ債の計算をやってみましょう。買付時の債券単価は、償還まで29年10か月（29.833年）で利回り（年複利）は4.2％で買った訳ですから

売付時の債券単価は、1年後すなわち償還まで28.833年のものを利回り2.4％で売却したのですから、

債券単価は、29.306から50.469と1.72倍となっています。

 
今のお金と将来のお金を同じテーブルに乗せることはできませんが、利回りという割引率で将来のお金を割引けば、今のお金と同じテーブルに乗せることができます。逆に言えば、今のお金も利回りによって増やしてやれば将来のお金と同じテーブルに乗せることができます。

今回のまとめ

◎債券の単価は、将来受取る利息・償還金を利回り（割引率）で割引いたものである。
◎利回り（割引率）を使えば、異時間のお金を同じテーブルに乗せることができる。

（次回につづく）